题目
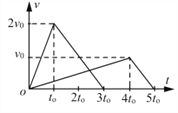
质量相等的A、B两物体放在同一水平面上，分别受到水平拉力F1、F2的作用而从静止开始做匀加速直线运动。经过时间t0和4t0速度分别达到2v0和v0 时，分别撤去F1和F2，以后物体继续做匀减速直线运动直至停止。两物体速度随时间变化的图线如图所示。设F1和F2对A、B的冲量分别为I1和I2，F1和F2对A、B做的功分别为W1和W2，则下列结论正确的是（ ）
A. I1:I2=12:5，W1:W2=6:5
B. I1:I2=6:5，W1:W2=3:5
C. I1:I2=3:5，W1:W2=6:5
D. I1:I2=3:5，W1:W2=12:5
可圈可点用户
2021-07-07 12:25
支付解锁查看解析>
优质解答
答案
C
解析
从图象可知，两物块匀减速运动的加速度大小之都为
，根据牛顿第二定律，匀减速运动中有
，则摩擦力大小都为
．根据图象知，匀加速运动的加速度分别为
，根据牛顿第二定律，匀加速运动中有
，则
，故
；由图看出，撤去拉力后两图象平行，说明加速度，由牛顿第二定律分析则知加速度
，说明两物体与地面的动摩擦因数相等，则两物体所受的摩擦力大小相等，设为f，对全过程运用动能定理得： 
， 
，得
， 
，图线与时间轴所围成的面积表示运动的位移，则位移之比为6：5，整个运动过程中
和
做功之比为
，故C正确．
可圈可点用户
2021-07-07 17:25