答案

SSS

解析

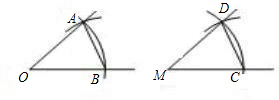
①设已知角的顶点为O，以O为圆心，任意长度为半径画圆，交角两边为A，B两点；

②用直尺画一条射线，端点为M，以M为圆心，用同样的半径画圆，该圆为圆M，交射线为C点；

③以A为圆心，以AB为半径画圆，然后以C点为圆心，以同样的半径画圆，交圆M于D，E两点，随意连MD或者ME；

得到的∠CMD就是所求的角；

由以上作角过程不难看出有三个对应边相等．

∴证明全等的方法是SSS．

故答案为：SSS．

三角形全等判定定理：

1、三组对应边分别相等的两个三角形全等(简称SSS或“边边边”)，这一条也说明了

三角形具有稳定性的原因。

2、有两边及其夹角对应相等的两个三角形全等(SAS或“边角边”)。

3、有两角及其夹边对应相等的两个三角形全等(ASA或“角边角”)。

4、有两角及一角的对边对应相等的两个三角形全等(AAS或“角角边”)

5、直角三角形全等条件有：斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边，直角边”) 所以：SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。

注意：在全等的判定中，没有AAA和SSA，这两种情况都不能唯一确定三角形的形状。