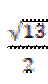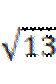题目

已知F1,F2是双曲线C的两个焦点,P为C上一点,且∠F1PF2=60°,|PF1|=3|PF2|,则C的离心率为( )
可圈可点用户
2021-06-08 11:54
支付解锁查看解析>
优质解答
答案
A
扩展知识
偏心率(离心率)椭圆两焦点间距离和长轴长度的比值。即某一椭圆轨道与理想圆环的偏离,长椭圆轨道“偏心率”高,而近于圆形的轨道“偏心率”低。离心率定义为椭圆两焦点间的距离和长轴长度的比值。双曲线的e>1。椭圆的0<e<1。
在椭圆的标准方程X^2/a^2+Y^2/b^2=1中,如果a>b>0焦点在X轴上;如果b>a>0焦点在Y轴上。这时,a代表长轴b代表短轴 c代表两焦点距离的一半,存在a^2=c^2+b^2。偏心率e=c/a (0<e<1)中,当e越大,椭圆越扁平。
可圈可点用户
2021-06-08 16:54