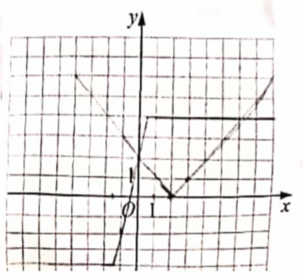
答案

当x≤-3/2时，2x+3≤0，2x-1≤0

g(x)=-(2x+3)+(2x-1)=-4

当-3/2<x<1/2时，2x+3>0，2x-1<0

g(x)=2x+3+2x-1=4x+2

当x≥1/2时，2x+3>0，2x-1≥0

g(x)=2x+3-(2x-1)=4

f(x+a)≥g(x)?|x+a-2|≥g(x)?|2-a+a-2|≥g(2-a)

?g(2-a)≤0 有图像可知2-a≤-1/2?a≥5/2

∴a+1/2≥3?f(1/2+a)≥g(1/2)?a+1/2-2≥4?a≥11/2

下证当a≥11/2时，f(x+a)≥g(x)

当x≤-1/2，g(x)≤0≤f(x+a)

当-1/2≤x≤1/2时，g(x)=4x+a

x+a≥-1/2+a≥-1/2+11/2=5?f(x+a)=|x+a-2|=x+a-2

x+a-2-（4x-2）=a-3x-4≥11/2-3*1/2-4=0

综上，a取值范围为[11/2，+∞)

扩展知识

一般的，在一个变化过程中，假设有两个变量x、y，如果对于任意一个x都有唯一确定的一个y和它对应，那么就称x是自变量，y是x的函数。x的取值范围叫做这个函数的定义域，相应y的取值范围叫做函数的值域。