中考数学旋转题型 中考数学旋转解题技巧
经典例题1、菱形与旋转问题
在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.
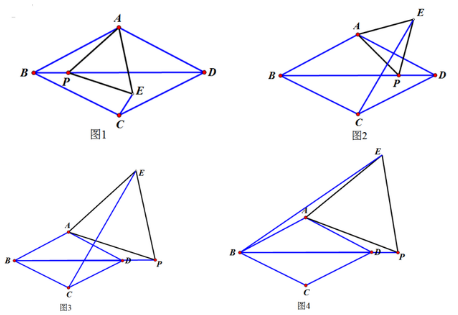
(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是________,CE与AD的位置关系是________;
(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);
(3)如图④,当点P在线段BD的延长线上时,连接BE,若AB=2√3,BE=2√19,求四边形ADPE的面积.
【试题分析】此题是四边形的综合题,重点考查菱形的性质、等边三角形的性质、全等三角形的判定与性质、勾股定理、以及图形的面积等知识点,解题的关键是正确地作出解题所需要的辅助线,将菱形的性质与三角形全等的条件联系起来,此题难度较大,属于考试压轴题.
(1)连接 AC ,根据菱形的性质和等边三角形的性质证明△ BAP ≌ CAE 即可证的结论;
(2)(1)中的结论成立,用(1)中的方法证明 △ BAP≌△ CAE 即可;
(3)连接 AC 交 BD 于点 O ,由 LBCE =90,根据勾股定理求出 CE 的长即得到 BP 的长,再求 AO PO 、 PD 的长及等边三角形 APE 的边长,可求得△ APD 和△ APE 的面积,进而求得四边形 ADPE 的面积.
【参考答案】(1)BP=CE CE⊥AD ;(2)成立;(3)8√3.
经典例题2、正方形中的三角形与旋转问题
(1)如图1,正方形ABCD中以AB为边在正方形内构造等边△ABE,等边△ABE边AE交正方形对角线BD于F点,求证:BF/FD=√3.
(2)将等腰Rt△BEF绕B点旋转至如图2的位置连接DE,M点为DE的中点,连接AM、MF,求MA与MF的关系;
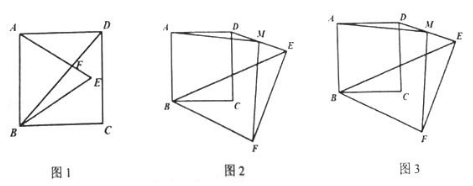
(3)如图3,将△BEF绕B点旋转一周,若EF=4,AB=1,请直接写出点M在这个过程中的运动路径长为 .
【试题分析】(1)延长AE,交CD于点G,由“8字”型相似可得BF:FD=DG:AB=tan60°=√3.(2)MA⊥MF,且MA=MF;
经典例题3、正方形中的线段与旋转问题
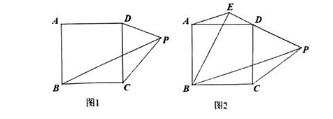
将正方形ABCD的边CD绕点C顺时针旋转α(0<α<90)至CP,连接PB,PD.
(1)如图1,当α=40°时,直接写出∠BPD的大小;
(2)如图2,过B作BE⊥PD交PD延长线于点E,连接AE.
①求∠BPD的大小;
②探究AE,PD之间的数量关系,并证明你的结论;
③当点D为PE中点时,PB=6,直接写出四边形ABPE的面积.
参考答案见下图

例题4、正方形与旋转问题
如图1,四边形ABCD为正方形,将△ACD绕点C顺时针旋转至△A1CD1的位置,旋转角为α.连接AA1,E为AA1的中点.
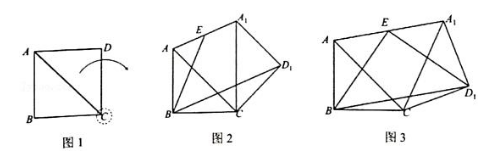
(1)当α=45°时,如图2,此时∠AA1C= ;
(2)在(1)的条件下,再将△EAB绕点E旋转180°至△EA1M的位置.请你在图2中完成作图,并证明:EC=EM;
(3)将△ACD绕点C顺时针旋转至如图3所示的位置,试判断△EBD1的形状并证明.
【参考答案】(1)67.5°;(2)略;(3)等腰直角三角形。